Tato kapitola nás seznámí s problematikou Vennových diagramů a přiblíží nám praktické využití těchto grafů. Jsou pojmenovány podle anglického vědce a kněze Johna Venna.

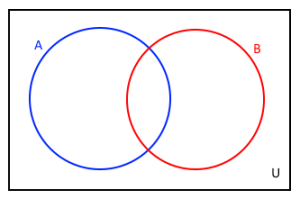
 Pomocí Vennova diagramu jsme schopni zobrazit libovolný počet množin a provádět na nich matematické operace. Základem Vennových diagramů je univerzum, které obsahuje všechny myšlené prvky. V rámci tohoto univerza pak můžeme vytvářet jednotlivé množiny. Protože nelze vytvořit žádnou množinu mimo univerzum, označuje se někdy univerzum i jako základní množina. Na následujícím obrázku vidíme univerzum U, které obsahuje dvě množiny A a B.

 Inkluze a disjunkce

Na následujících grafech si ukážeme neostrou inkluzi množin a disjunkci množin pomocí Vennových diagramů.

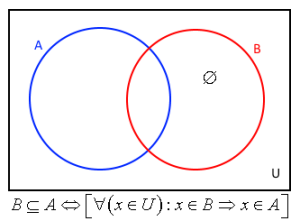
První obrázek nám ukazuje neostrou inkluzi množin.

Množina B je podmnožinou množiny A tehdy, a jen tehdy, když pro všechny prvky x, které jsou součástí univerza U platí: každé x, které náleží do množiny B přísluší x, které náleží do množiny A.

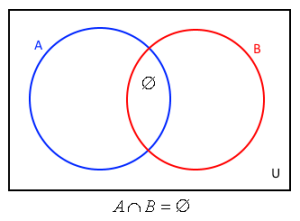
Druhý obrázek nám ukazuje disjunkci množin zachycenou Vennovým diagramem.

Vennův diagram nám ukazuje, že průnik množin A a B je prázdná množina.

Základní operace

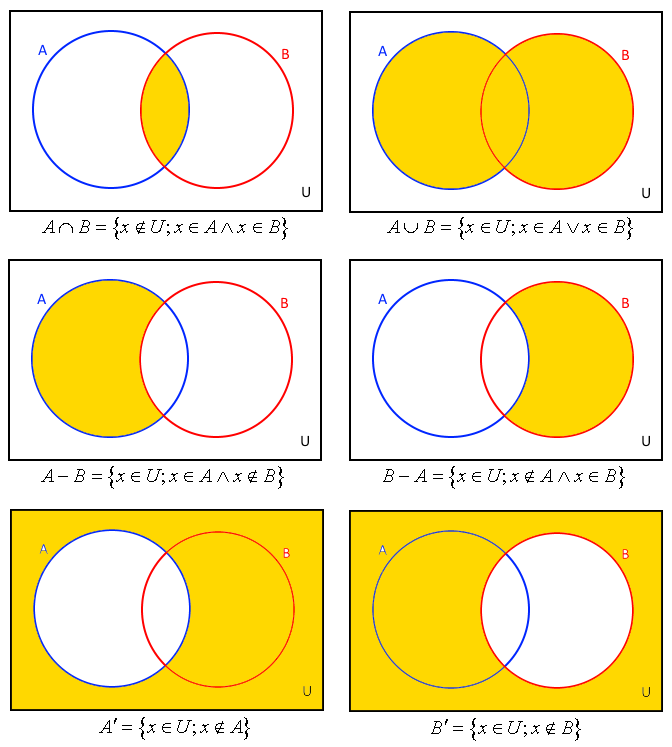
Základní operace množin, jako je průnik, sjednocení, rozdíl či doplněk, můžeme znázornit i pomocí Vennových diagramů.

Vícemnožinové Vennovy diagramy

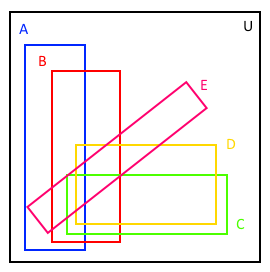
Vennovy diagramy můžeme aplikovat i na univerzum, které obsahuje více než jen dvě množiny. Následující příklady ukazují složitější Vennovy diagramy. Jejich nevýhodou bývá menší přehlednost s narůstajícím počtem množin.

3 množiny v rámci univerza

4 množiny v rámci univerza

5 množin v rámci univerza

M.P.