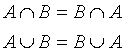V této kapitole si vysvětlíme základní matematické operace s množinami, jako je průnik, sjednocení, rozdíl či doplněk.
Průnik množin
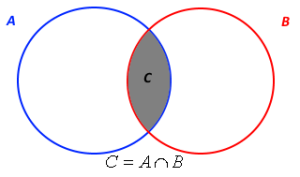
Prvky, které jsou obsaženy jak v množině A, tak i v množině B, označujeme jako průnik množin. Pro označení průniku v matematice používáme symbol 
. Matematicky můžeme vyjádřit stav, kdy množina C je průnikem množin A a B, následovně:
a graficky pak takto:
PRO CHYTRÉ HLAVY: Množiny A a B jsou disjunktní, pokud nemají žádný společný prvek. Průnikem těchto množin je tedy prázdná množina 
. Například množina
a množina
jsou disjunktní. Graficky můžeme zobrazit následovně:
Sjednocení množin
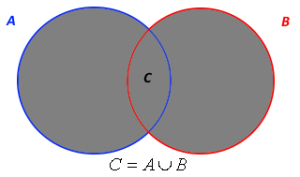
Prvky, které jsou obsaženy buď v množině A nebo v množině B, označujeme jako sjednocení množin. Pro označení sjednocení v matematice používáme symbol 
. Matematicky můžeme vyjádřit stav, kdy množina C je sjednocením množin A a B, následovně:
a graficky pak takto:
Rozdíl množin
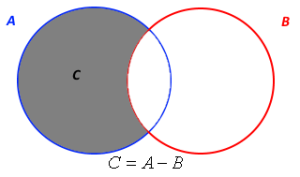
Prvky, které jsou obsaženy v množině A a zároveň nejsou obsaženy v množině B, označujeme jako rozdíl množin. Pro označení rozdílu v matematice používáme symbol mínus. Matematicky můžeme vyjádřit stav, kdy množina C je rozdílem množin A a B, následovně:
a graficky pak takto:
Doplněk množiny
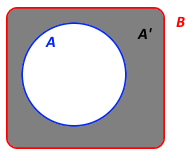
Máme-li množinu B a její podmnožinu A, pak prvky, které nejsou obsaženy v množině A, ale zároveň jsou v množině B, označujeme jako doplněk množiny. Pro označení doplňku v matematice používáme symbol čárka. Matematicky můžeme vyjádřit stav, kdy množina A‘ je doplňkem množiny A vzhledem k množině B, následovně:
a graficky pak takto:
PRO CHYTRÉ HLAVY: U některých operací s množinami můžeme nalézt zajímavé vlastnosti. Například průnik a sjednocení je komutativní operace. To znamená, že nezáleží na pořadí prvků (to známe již ze sčítání a odečítání). Platí tedy následující:
M.P.