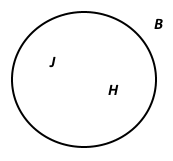
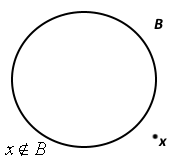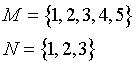V této kapitole si jednoduše vysvětlíme, co je to množina, a co všechno s ní můžeme v matematice dělat. Představme si batoh, který nazveme písmenem B, a uvnitř bude jablko J a hruška H. V matematice bychom mohli říct, že jsme vytvořili množinu B, která obsahuje prvky J a H.
Každý prvek, který množina obsahuje může být buď číslo anebo další množina. Zastavme se u první varianty, a to čísel. Množina může obsahovat jakákoliv čísla, ale vždy pouze jen jednou. Žádné číslo nemůže být uvedeno v množině dvakrát. Buď množina číslo obsahuje nebo ne. Jiná varianta není.
Pokud prvek x není součástí množiny M (nenáleží do množiny M), značíme:
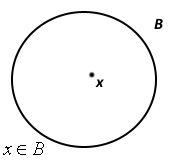
Můžeme použít i grafické znázornění toho, zdali nějaký prvek do množiny patří či nikoliv.
Všechny prvky, které jsou zobrazeny vevnitř kružnice, jsou zároveň prvky množiny B. Naopak prvky, které jsou vně kružnice, již nejsou obsaženy v množině B.
Obsah množiny můžeme určit dvěma způsoby. Buď vypíšeme všechny prvky, které množina obsahuje,
anebo množinu určíme pomocí charakteristických vlastností prvků, které obsahuje. V našem případě tedy jako množinu přirozených čísel 
, které jsou nižší než hodnota 6.
Podmnožina – Inkluze
Stejně tak i množina může být obsažena v jiné množině. Pokud je množina N obsažena v množině M, pak říkáme, že N je podmnožinou množiny M. Tedy:
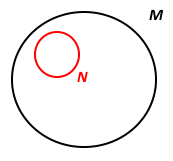
V odborné matematice se vztahu „být podmnožinou“ říká INKLUZE. Na následujícím příkladu si ukážeme množinu M a její podmnožinu N, které jsou definovány
a zobrazeny následovně:
PRO CHYTRÉ HLAVY: Rozlišujeme ostrou a neostrou inkluzi. Neostrou inkluzi jsme si vysvětlili výše, připouští, že množina si může být s podmnožinou rovna. Ostrá inkluze již neumožňuje rovnost množiny s podmnožinou a značí se 
. U ostré inkluze nazýváme podmnožinu jako vlastní, u neostré pak jako podmnožinu nevlastní.
Rovnost množin
Množiny A a B jsou si vzájemně rovny, pokud obsahují naprosto stejné prvky. V matematice to značíme klasicky rovnítkem. Uvědomme si, že vlastně platí, že množina A je podmnožinou množiny B a zároveň množina B je podmnožinou množiny A.
Takže množina A je rovna množině B tehdy a jen tehdy, když množina A je podmnožinou množiny B a zároveň množina B je podmnožinou množiny A.
M.P.